WGS84 (World Geodetic System of 1984)
Polar coordinates (longitude, latitude, height above mean sea level) are used as a standard technique of indicating positions for worldwide navigation. Most commercial GNSS receivers also output their measured positions in this format.
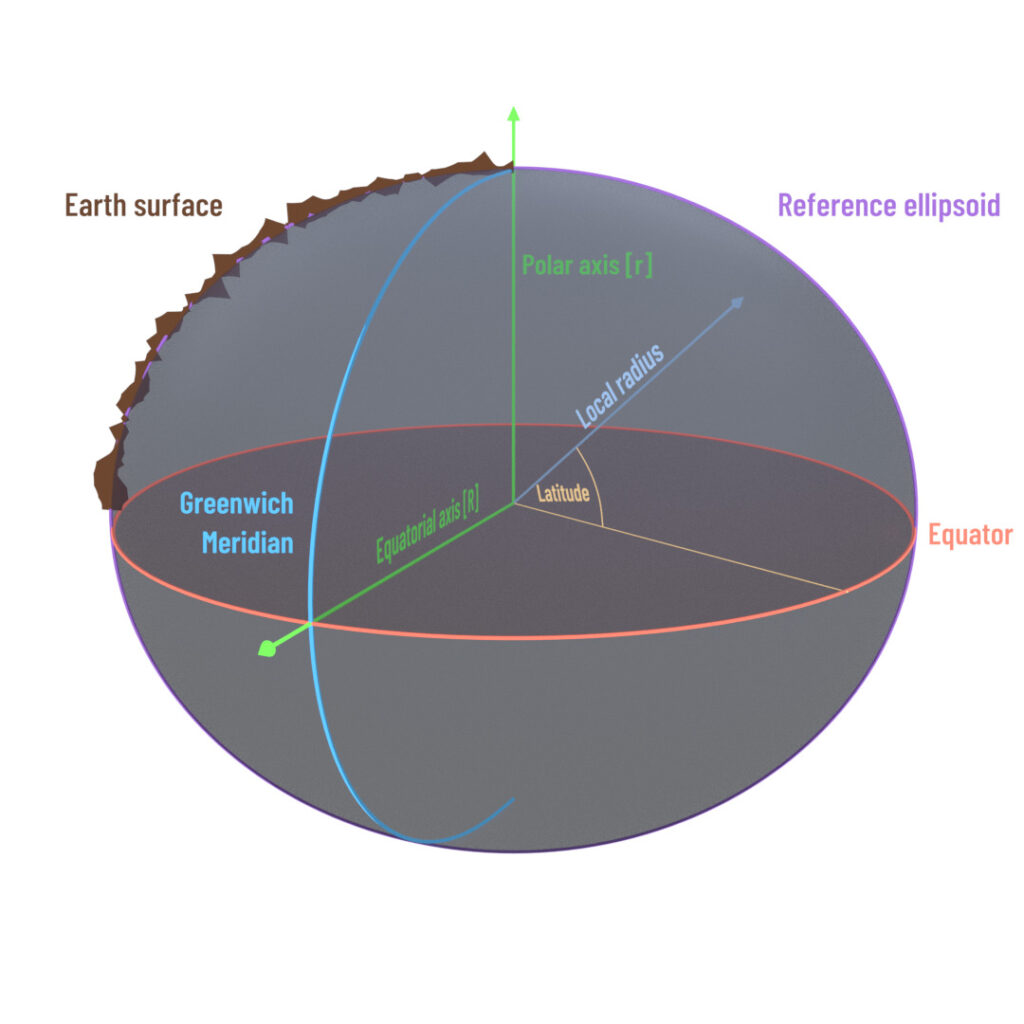
Such position details are based on mathematical models of the earth, the WGS84 being the best known and most common frame of reference among them. The WGS84 represents an ellipsoid possessing rotational symmetry (see the illustration below).
The zero meridian (0° longitude) passes through Greenwich, England; 0° latitude is the equator.
WGS84 does not specify a height, but a location-dependent radius which follows an ellipse function dependent on the degree of latitude.
The local radius at the equatorial axis = R. As the degree of latitude increases, this radius changes to approach a value = r at the poles.
ETRS89 (European Terrestrial Reference System)
The European Terrestrial Reference System 1989 (ETRS89) is an ECEF (Earth-Centred, Earth-Fixed) geodetic Cartesian reference frame, in which the Eurasian plate as a whole is static. The coordinates and maps in Europe based on ETRS89 are not subject to change due to the continental drift.
Since then ETRS89 and ITRS diverge due to the continental drift at a speed about 2,5 cm per year. By the year 2000 the two coordinate systems differed by about 25 cm.
Note: It is a common practice for the European reference network operators to configure the coordinates of their ground reference stations expressed in ETRS89 datum instead of WGS84. By using a European reference network, the output of the receiver will be expressed in ETRS89 reference frame.
Height value
Height values are usually based on geoide reference surfaces. One such surface is the mean sea level (MSL), described best as a surface exhibiting a constant gravity at all points. In most countries, this surface (MSL) serves as a zero-point for height indications.
The WGS84 reference model described in the previous chapter only specifies the radius “R” from the ellipsoid’s center. The difference between the ellipsoid and MSL is termed “Undulation” and is generally < 100 m across Europe. This undulation is calculated by most receivers locally or listed internally in a chart, both based on the EGM96. The ADMA indicates the height in MSL.

EGM96 – Global Geoid Model
The EGM96 is a mathematical model of the Earth’s gravity field. From this gravity field model, it computes the geoid — a surface that represents mean sea level (MSL) across the entire Earth.
The model provides a value called geoid height (undulation, N) at any location on Earth.
This is the offset between the ellipsoid (WGS-84) and mean sea level.
The ADMA systems use two different GNSS receiver types (NovAtel and u-blox). Both receivers are based on the EGM96 geoid model, which provides geoid height values at specific latitude / longitude points stored in a grid. NovAtel uses a high resoluation grid (0.5°×0.5°), while u-blox uses a coarser low resolution grid (10°×10°). The grid allows the receiver to look up the geoid height at a given location to convert GPS ellipsoid heights (h) into mean sea level heights (H) using the formula H = h – N. A finer grid captures local variations more accurately, so the computed heights can differ slightly between receivers depending on position.




